Physics Simulator from Scratch

Project: Physics Simulator

The objective of this project was to create a physics simulator from scratch for rigid bodies. Using python sympy, numpy and plotly a simulator was created for two topics: Jack in the Box and a Trebuchet.

Project Description: Jack in the Box Simulation

System Overview: The simulation involves two main components - a jack and a box, both modeled as squares. These components have specific transformations and frames, crucial for analyzing their movements.

System Modeling: The system’s transformations are described using matrices representing rotations and translations for both the box and the jack. These transformations are essential for calculating kinetic and potential energies.

The free body diagram with the locations of the frames is as follow:

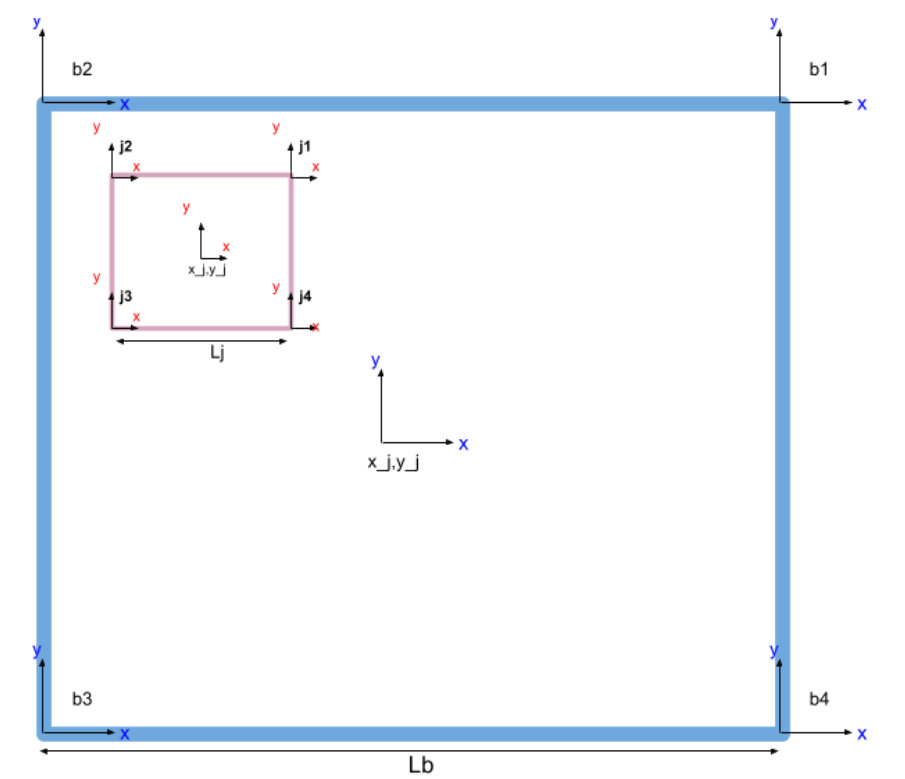
Theoretical Analysis:

• Kinetic Energy (KE) and Potential Energy (PE): Using the transformation matrices and mass calculations for the jack and box, KE and PE are computed. KE is determined using the velocity calculated from the transformation matrix at the centroid of both components. PE is derived from the vertical position in the transformation matrix multiplied by the total weight of the body.

• Lagrangian Equations: The Lagrangian equations, L = KE - PE, are employed. To solve the equations of motion, Lagrangian derivatives with respect to configuration variables are utilized. Translation force and torque are applied to specific components, and the resulting forced Euler-Lagrange equations are solved.

• Constraints and Impacts: Sixteen constraints are imposed to ensure the jack stays within the box. These constraints serve as impact updates, triggered when contact occurs. Impact update equations are calculated based on the constraints and involve solving equations to determine velocities and lambda (an impact variable).

Code Implementation: The simulation successfully portrays the interaction between the jack and the box. The jack falls into the box, collides with the walls, and experiences rotations due to applied forces. Multiple impacts occur, impacting the simulation’s dynamics before it concludes.

Video:

Project Description: Trebuchet Simulation

System Overview: The project involves simulating a trebuchet, an ancient siege engine used for hurling projectiles. It comprises various components such as the throwing arm, counterweight, sling, and base structure.

System Modeling: Modeling the trebuchet includes defining the geometries and transformations of its components. These transformations, including rotations and translations, are pivotal for calculating the trebuchet’s motion and energy dynamics.

The free body diagram with the locations of the frames is as follow:

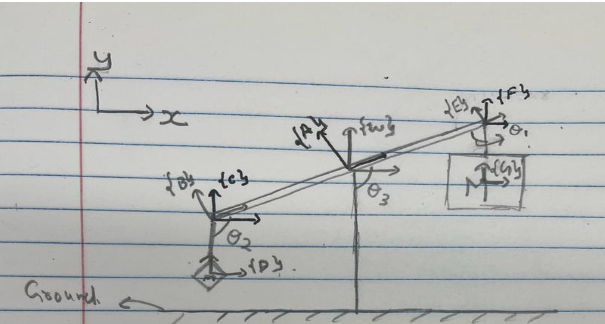
Theoretical Analysis:

• Energy Calculations: The simulation calculates potential and kinetic energies of the trebuchet during its operation. The potential energy stored in the raised counterweight and the resulting kinetic energy of the projectile at release are computed using physical principles.

• Lagrangian Equations: The Lagrangian formulation is employed to derive the trebuchet’s equations of motion. The system’s dynamics, incorporating potential and kinetic energies, are expressed using Lagrangian mechanics to understand its behavior.

• Constraints and Dynamics: One crucial constraint is x=0, representing the projectile’s release point. This constraint significantly influences the trebuchet’s dynamics.

Code Implementation: The simulation effectively illustrates the functioning of a trebuchet. It demonstrates the release of the projectile, the rotation of the throwing arm, and the impact of various parameters on its trajectory. The simulation provides insights into the mechanical aspects and behaviors of this historical siege engine.

Video:

The code can be found at this github link